行测数量关系练习题

  1、一个水库在年降水量不变的情况下，能够维持全市12万人20年的用水量。在该市新迁入3万人之后，该水库只够维持15年的用水量。市政府号召节约用水，希望能将水库的使用寿命提高到30年。那么该市市民平均需要节约多少比例的水才能实现政府制定的目标?

  2、一个长方体的长、宽、高恰好是三个连续的自然数，并且它的体积数值等于它的所有棱长之和的2倍，那么这个长方体的表面积是多少?

  A.74 B.148 C.150 D.154

  3、纽约时间是香港时间减13小时，你与一位在香港的朋友约定，香港时间6月1日晚上8时与他通电话，那么在纽约你应几月几日几时给他打了电话?

  A.6月1日上午7时 B.5月31日上午7时

  C.6月2日上午9时 D.6月2日上午7时

  4、某公司举办年终晚宴，每桌安排7名普通员工与3名管理人员，到最后2桌时，由于管理人员已经安排完，便全部安排了普通员工，结果还差2人才能刚好坐满。已知该公司普通员工人数是管理人员的3倍，则该公司有管理人员多少名?

  A.24 B.27 C.33 D.36

  5、甲每4天进城一次，乙每7天进城一次，丙每12天进城一次，某天三人在城里相遇，那么三人下次相遇至少需要多少天?

  A.12天 B.28天 C.84天 D.336天

  6、某项工程计划300天完成，开工100天后，由于施工人员减少，工作效率下降20%，问完成该工程比原计划推迟多少天?

  A.40 B.50 C.60 D.70

答案详细解析

  1、【答案】A。解析：“牛吃草”问题。设年降水量为x，每万人每年原用水量为1，平均节约用水的比例为y，则有(12-x)×20=(12+3-x)×15=[(12+3)(1-y)-x]×30，解得。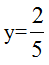

  2、【答案】B。解析：设该长方体的长、宽、高分别是a，a-1，a+1。那么有(a-1)a(a+1)=2×4[(a-1)+a+(a+1)]，整理得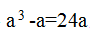，求得a=5。所以这个长方体的表面积为2(a+1)a+2(a-1)a+2(a+1)(a-1)=148。

  3、【答案】A。解析：香港时间6月1日晚上8时就是20时，此时纽约时间应是20-13=7时，即6月1日上午7时。

  4、【答案】B。解析：最后两桌安排了10+8=18名普通员工。设之前安排了x桌，则管理人员有3x人，普通员工有7x+18人。7x+18=3×3x，解得x=9，该公司有3×9=27名管理人员。

  5、【答案】C。解析：此题可看成求4、7、12的最小公倍数问题，显然84为正确答案。

  6、【答案】B。解析：根据效率与时间成反比，可得正常200天的工作，效率下降后需要200÷(1-20%)=250天，故需推迟50天。