行测数量关系练习题

  1、 a大学的小李和b大学的小孙分别从自己学校同时出发，不断往返于a、b两校之间。现已知小李的速度为85米/分钟，小孙的速度为105米/分钟，且经过12分钟后两人第二次相遇。问a、b两校相距多少米?

  A.1140米 B.980米 C.840米 D.760米

  2、将一个表面积为18平方厘米的正方体沿对角线切成两块对称的三棱柱(见下图)，并将这两块三棱柱重新拼接成一个大的三棱柱。则这个大三棱柱的表面积最大为多少平方厘米?

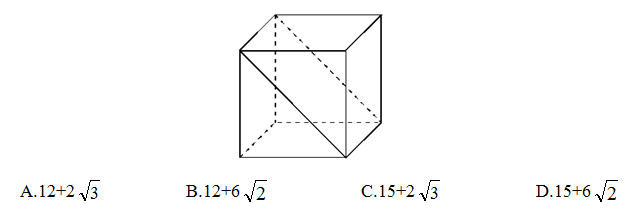
  3、“红星”啤酒开展“7个空瓶换1瓶啤酒”的优惠促销活动。现在已知张先生在活动促销期间共喝掉347瓶“红星”啤酒，问张先生最少用钱买了多少瓶啤酒?

  A.296瓶 B.298瓶 C.300瓶 D.302瓶

  4、有一批书，分给公司的所有人，若每人一本，则还差19本，若每个部门派7本，则多出1本，如果再招聘2个人进公司，则正好每个部门有9人，问：总共有多少个部门?

  A.11 B.9 C.7 D.5

  5、 在一条新修的道路两侧各安装了33座路灯，每侧相邻路灯之间的距离相同。为提高照明亮度，有关部门决定在该道路两侧共加装16座路灯，要使加装后相邻路灯之间的距离也相同，最多有多少座原来的路灯不需要挪动?

  A.9 B.10 C.18 D.20

  6、工厂需要加工一批零件，甲单独工作需要96个小时完成，乙需要90个小时，丙需要80个小时，现在按照第一天甲乙合作，第二天甲丙合作，第三天乙丙合作的顺序轮班工作，每天工作8小时，当全部零件完成时，甲工作了多少小时?

  A.16 B.24 C.32 D.44

答案详细解析

  1、【答案】D。解析：设A大学和B大学之间的距离为s，因为小孙和小李相遇两次，则两人走过的路程总共为3s，根据题意可得：12×(85+105)=3s，解得s=760米。选D。

  2、【答案】D。解析：

  3、【答案】B。解析：6个空瓶可以换一个瓶子里面的啤酒，故买6瓶酒可以喝7瓶。347÷7=49……4，则应买49×6+4=298瓶。

  4、【答案】A。解析：设总共有x个部门，则9x-2-19=7x+1，解得x=11，答案为A。

  5、【答案】C。解析：最初在道路一侧安装33座路灯有33-1=32个间隔，设每个间隔距离为m。共加装16座路灯，则每侧加装8座，每侧共有33+8-1=40个间隔，设每个间隔距离为n。则32m=40n，得出4m=5n。求最多则间隔尽可能小，故m=5，n=4。所以每侧有40×4÷(4×5)+1=9座路灯不需要移动，则两侧最多有2×9=18座原来的路灯不需要挪动。

  6、【答案】C。解析：根据题意，令工作总量为1440(96、90、80的最小公倍数)，甲每小时的工作量为15，乙每小时的工作量为16，丙每小时的工作量为18，如果按照题干要求分配，每天工作8小时，那么前三天的总工作量应为2×8×(15+16+18)=784，大于总量的一半，因此工作将在第四天、第五天或第六天完成。第四天工作量为8×(15+16)=248，第五天工作量为8×(15+18)=264，此时依然有工作剩余，因此可知工作将在第六天完成，甲在第六天不工作，因此工作完成时，甲一共工作了4天，工作时间为4×8=32小时。