利润问题是行测数量关系考试中的常见考点，部分考生觉得这类题型题干信息和条件多，做起来比较慢。如果我们能够掌握一定的方法和技巧，将有助于我们解题。在此给大家介绍一下如何巧用特值法解决利润问题。

  【例1】某家具店购进一批桌椅，每套进价200元，按期望获利50%定价出售。卖掉这批桌椅的60%以后，店主为提前收回资金，打折出售余下的桌椅。售完全部桌椅后，实际利润比期望利润低了18%。问余下的桌椅是打几折出售的?

  A.七五折 B.八二折 C.八五折 D.九五折

  【解析】C。本题中桌椅的销量无实际值，而是以百分数的形式给出相关条件，不妨设这批桌椅的总量为10，打折后出售的价格为x。由题意，整理相关信息如下：

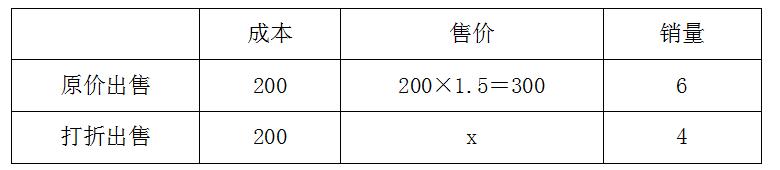
  根据实际利润比期望利润低了18%，有(300-200)×6+4(x-200)=(300-200)×10×(1-18%)，解得x=255。因此打折后出售的价格为255元，255÷300=0.85，即余下的桌椅是打八五折出售的，故本题选C。

  【例2】一批货物，本来按获得50%的利润来定价。结果只卖出70%的货物，为尽早卖出余下的货物，商店决定按定价打折销售，这样所获得的全部利润，是原来的期望利润的82%，问打了多少折?

  A.2.5折 B.5折 C.8折 D.9折

  【解析】C。本题没有给我们关于价格和销量具体的数值，只以百分数的形式给出相关条件，我们不妨设货物的成本价为100，这批货物的总量为10，打折后出售的价格为x，由题意，整理相关信息如下：

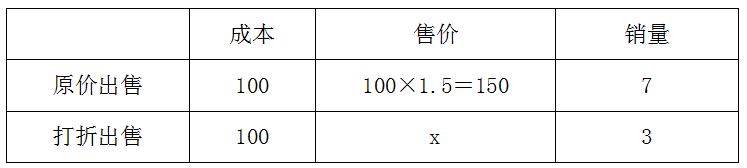
  根据所获得的全部利润是原来所期望利润的82%，有(150-100)×7+(x-100)×3=(150-100)×10×82%，解得x=120。因此打折后的售价为120元，120÷150=0.8，即打了8折，故本题选C。

  思路点拨：在利润问题中，通常会涉及成本、售价、销量、利润、利润率和折扣这些基本概念。如果条件比较复杂，可以通过列表梳理各个概念间的关系。同时，我们还可以结合特值法简化计算过程：

  1.价格无实际数值，且价格间关系表示为倍数、分数或百分数形式，可设成本或售价为特值;

  2.销量无实际数值，且销量间关系表示为倍数、分数或百分数形式，可设销量为特值。

  最后，提醒各位考生，平时做题时多多总结，以提高对利润问题的概念以及如何设特值的敏感性。